Р.А. Симонов. О вычислительной арифметике
Специальное изучение средневекового облика древнерусских математических знаний связано с исследованиями ряда советских историков. Важна работа И. Г. Спасского по истории русских счетов, по характеру используемых источников касающаяся в основном XVI—XVII вв. Академик Б. А. Рыбаков дал интересную интерпретацию сведений о возможном геометрическом средстве древнерусских зодчих; его исследование относится к воссозданию облика средневековой архитектурной математики. М. П. Сотникова открыла неизвестную ранее форму записи чисел на серебряных плательных слитках. Она поставила вопрос о существовании особой «практической арифметики», которую применяли в Древней Руси для расчета сырья при выплавке гривен.
Наименее разработанной областью остаются древнерусские арифметические представления XI—XIII вв. о вычислительных операциях в их средневековом облике. Ценные результаты, полученные учеными, либо относятся к более позднему времени (И. Г. Спасский), либо касаются геометрических знаний (Б. А. Рыбаков), либо относятся к особой категории арифметических представлений (М. П. Сотникова).
Арифметические навыки в вычислениях в той или иной степени могли отразиться в сохранившихся памятниках письменной и материальной культуры. Критерием для отбора может служить наличие определенных числовых характеристик. Числовые записи встречаются в основном тексте рукописей и в различных приписках, в виде единичных цифровых пометок, а также в особых математических текстах. Цифры содержатся в надписях на камнях, стенах сооружений, на ремесленных изделиях и предметах художественного творчества, включая произведения штемпельной техники, например печати. Значительно расширился круг источников об использовании арифметических представлений в быту человека Древней Руси благодаря открытию берестяных грамот. Материальным средством, тесно связанным с арифметическими представлениями, являются деньги.
Анализ особенностей денежной системы может дать интересный материал об употреблявшейся в соответствующее время вычислительной практике. Недаром ведь говорят: «Деньги счет любят».
Древнерусских письменных документов в подлинниках от XI—XIII вв. дошло сравнительно мало. Это осложняет изучение вычислительных навыков на Руси периода, предшествующего татаро-монгольскому нашествию. Однако источники математического характера, восходящие к указанному периоду, сохранились в позднейших списках. Одним из них является хронолого-математическое сочинение новгородца Кирика «Учение им же ведати человеку числа всех лет», написанное в 1136 г., но известное по спискам XVI—XIX вв.
Кроме того, в некоторых текстах (XV и последующих веков) Карамзинской группы списков Пространной редакции «Русской Правды» встречаются в качестве добавления своеобразные задачи с числовыми результатами порядка сотен тысяч. Сведения, которые сопутствуют числам, дают основания для выводов о том, как эти числа могли быть получены в наше время. Вопрос же о том, каким образом они были вычислены древнерусскими математиками, остается открытым. Вот что об этом говорит советский историк В. К. Кузаков: «И хотя авторам «Русской Правды» приходилось умножать только на 2, 6 и 10 и делить лишь на 50, до сих пор не установлено, каким образом проводились эти исчисления»3.
Каким образом можно воссоздать существо древнерусского вычислительного метода в его средневековом облике? Очевидно, соответствующая реконструкция должна учитывать особенности математического просвещения средневековья и основываться на сопоставлении данных древнерусских источников с вычислительными приемами и средствами византийцев и других соседних народов.
С древности в Европе и странах Востока были распространены различные наглядно-механические приспособления для выполнения арифметических подсчетов. Суть их состояла в перекладывании, или механическом перемещении, по особым правилам счетных элементов на вычислительном «поле». В качестве такого «поля» могла использоваться поверхность стола, скамейки, доски, пола или земли. Существовали переносные постоянного назначения вычислительные «поля». Счетными элементами в зависимости от вида наглядно-вычислительного приспособления могли быть камешки, косточки от слив и вишен, бобы и другие мелкие предметы. А также — особые счетные жетоны, с цифровыми обозначениями или без них. Счетные элементы могли использоваться «в россыпи» и нанизанными на прутья или шнуры. Такого рода приспособления, состоящие из вычислительного «поля» и счетных элементов, имеют общее название — абак. Абак существовал в Древнем Египте и античной Греции, возможно, он был у вавилонян. В архаических вариантах абака вычислительное «поле» и счетные элементы не были соединены вместе, как, например, наши так называемые конторские счеты. Древний абак состоял как бы из двух обособленных компонентов: вычислительной доски и счетных элементов «в россыпи». В 1848 г. на острове Саламине была обнаружена такая вычислительная доска, сделанная из мрамора, относящаяся к древнегреческому периоду.
Если на Руси в домонгольское время употреблялся архаический абак, то соответствующий счет мог сохраниться в позднейшее время если не в чистом, то в каком-то преобразованном виде.
Какие есть на этот счет данные?
Известно, что в XVI в. у нас употреблялся так называемый «дощаный счет», превратившийся вскоре в счеты типа конторских. Следует иметь в виду, что «дощаный счет» был оригинальным и отличался от западноевропейского «счета на линиях», сложившегося в XIII в. Последний имел широкую известность в Европе и, по-видимому, применялся в западных русских областях, входивших временно в состав Полыни и Великого княжества Литовского.
И. Г. Спасский обратил внимание на иностранные свидетельства XVI—XVII вв., в которых счетные умения русских характеризуются так, что их нельзя свести ни к «счету на линиях», ни к «дощаному счету». И. Г. Спасский указывает два таких текста. Первый принадлежит немцу Г. Штадену, который был опричником Ивана Грозного. Он имел возможность довольно подробно ознакомиться с русским бытом второй половины XVI в. Другой фрагмент содержится в записях А. Олеария, посетившего Россию в первой половине XVII в. И тому и другому бросилась в глаза одна и та же особенность русского вычислительного способа — применение плодовых косточек. Наблюдения иностранцев содержат интересные подробности: косточки были сливовые и вишневые, их носили в маленьком мешочке.
Отсюда можно заключить, что наблюдаемый иностранцами «счет костьми» отличался от западноевропейского «счета на линиях». Это не был и «дощаный счет», так как иностранцы не упоминают о рамах, в которых закреплялись счетные элементы на прутьях или шнурах. Свидетельство о ношении косточек в мешочках скорее говорит о том, что счетные элементы употреблялись «в россыпи».
Для окончательного решения вопроса нужно опираться непосредственно на древнерусские тексты, отражающие вычислительную практику домонгольской поры. Таким является упомянутый выше дополнительный материал «Русской Правды».
В Карамзинской группе списков «Русской Правды» он занимает место с 49-й по 69-ю статьи. Таких списков, древнейшие из которых относятся к середине XV в., насчитывается более десятка; все они однотипны, без существенных различий в содержании.
Указанные дополнительные статьи представляют собой набор своеобразных арифметических задач с пересчетом натуры на деньги. В них речь идет о приплоде скота, пчел и пр. за определенный период с подсчетами стоимости в древнерусской денежной системе.
Вместе с тем статьи-задачи из «Русской Правды» — важный исторический источник, содержащий данные о древнерусской «кунной» денежной системе, по которым она реконструируется: 1 гривна = 50 резанам = 20 ногатам.
Задачи с пересчетом натуры на деньги из «Русской Правды» в математическом отношении изучались неоднократно. Итог сводился к установлению обилия неточностей и несообразностей в числах. Тем не менее за наслоением кажущихся несообразностей советские математики Б. В. Гнеденко и А. П. Юшкевич разглядели определенное рациональное содержание. Они открыли в задачах интересную черту: в тех случаях, когда числовые данные не были слишком искажены, в основе условия проявлялась геометрическая прогрессия со знаменателем 2.
Бросается в глаза, что наряду с большим количеством неверных числовых данных в задачах содержатся почти безукоризненные результаты, если они касаются сведений о денежной системе.
Обычно ученые сортировали числовой материал дополнительных статей «Русской Правды» по задачам в целом. Задач, числовые данные в которых имели математический смысл, оказалось мало. Подавляющее большинство задач. оказывались забракованными вместе с содержащимся в них числовым материалом. А что, если поступить так: выбрать во всех упражнениях данные о ценах на товары и проанализировать их независимо от условий задач?
Результат исследования оказался следующим. Переводу натуры на деньги посвящены 8 вариантов подсчетов. Выделенные варианты подразделяются на две группы. К первой относятся 4 варианта, для их выполнения достаточно одной математической операции: числовой записи (условно — умножения на 1) , удвоения (умножения на 2), раздвоения (деления пополам) и утроения (умножения на 3). Ко второй группе отнесены варианты подсчетов (их также четыре), которые выполняются посредством последовательности 2—4 современных арифметических операций, из которых по крайней мере одна связана с действием деления. В соответствии с математическим существом первую группу условно можно назвать группой простейших подсчетов, а вторую — группой усложненных подсчетов.
С позиции нашей привычки к вычислениям на бумаге, видимой связи между обеими группами подсчетов не обнаруживается. Однако разделение именно на выделенные группы в средневековом источнике может быть вовсе не случайным.
Поэтому необходимо сделать анализ структуры подсчетов двух групп в соответствии с особенностями средневековых арифметических представлений. Подсчеты, которые кажутся на основе теперешних представлений несовместимыми по сложности арифметических операций, обнаруживают тесную связь между собой с позиции вычислений на абаке.
В этом смысле становится понятно, почему конечные результаты выражены в имевшей распространение в Древней Руси «кунной» денежной системе.
Архаический абак и его различные модификации, включая русские (конторские) счеты, были вычислительными приспособлениями для действий с именованными числами. В конструкции абака «программировалась» определенная денежная система, поэтому числовые значений, полученные на нем, как бы автоматически приобретали «денежную» форму выражения.
Таким образом, если в Древней Руси употреблялось наглядно-вычислительное приспособление (абак), то в нем должна была быть «запрограммирована» функционировавшая денежная система. Тексты, служившие целям овладения счетом с использованием абака, могли характеризоваться двойственным отношением к хозяйственно-финансовой «тематике», которое как раз представлено в статьях-задачах «Русской Правды». Хозяйственный быт в них отображен условно и неточно, а денежная система — правильно и полно. Итак, соображения о характере древнерусской вычислительной техники позволяют более правильно понять существо важнейшего исторического источника о «кунной» денежной системе — дополнительных статей Карамзинской группы списков «Русской Правды».
В памятниках материальной и письменной культуры, а также искусства Руси может еще в каких-то формах отразиться практика использования наглядно-вычислительного приспособления.
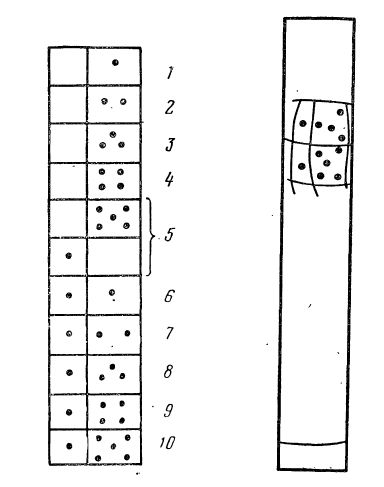
Рис. 1. Схема обозначений чисел на абаке
Рис. 2. Древнерусское пряслице XIII в. с записью типа домино (развертка). На абаке такая запись могла выражать число 100
В памятниках материальной культуры счет на абаке мог получить отражение в виде особой системы записи чисел типа домино. В Древней Руси числа выражались в «буквенной» нумерации, а также в виде засечек на серебряных гривнах (рассмотрено М. П. Сотниковой) или посредством групп точек (например, на гирьках, игральных костях и пр.). Среди «точечных» числовых записей можно выделить обозначение чисел в системе абака: при наличии двух частей (возможно, узкой и широкой), причем в одной из них (узкой) должно быть указано не более одной точки, а в другой (широкой) не более пяти. Возможная форма записи чисел от 1 до 10 в системе абака представлена на рис. 1. Такого рода опубликованное Л. А. Голубевой начертание типа домино встречается на пряслице XIII в. из Белоозера4 (рис. 2). Надпись соответствует двум последним уровням рис. 1. Если верно, что эта запись на пряслице дается в системе абака, то нижний ряд точек мог обозначать 10 (одна точка слева — 5, а еще 5 давали пять точек справа), верхний ряд точек мог выражать 90 (одна точка слева — 5 десятков, а еще 4 десятка давали четыре точки справа). Итого: 1 десяток + 9 десятков = 100.
Способы записи чисел (нумерация) были специальным объектом изучения или определенным атрибутом древнерусской математической культуры. Сохранились числовые берестяные грамоты XIII—XIV вв., представляющие собой фрагменты «цифровых алфавитов». Эти источники свидетельствуют о том, что древнерусская «кириллическая» нумерация была предметом школьного изучения в период татаро-монгольского ига.
Подтверждением существования операции раздвоения может служить структура многих древнерусских мер. Так, от названия меры земли «выть» шли ее доли: полвыти, четь (четверть выти), полчети, полполчети, полполполчети и т. д.; от полчети: осьмина, пол-осьмина; от четверика: полчетверик, полполчетверик, малый четверик, полмалый четверик. Древнерусская мера длины «сажень» делилась на доли по принципу 2, 4, 8, 16.
Интерес представляет древнерусское слово «сугубое», выражавшее удвоенное значение числа. Для примера можно указать следующий текст из тайнописи XVII в.: «присовокупляй троесотное сугубое з двоесотным к сим же и единосотное су[гу]бое», что значит: «прибавь 300 удвоенное к 200, к ним —сотню удвоенную», т. е. 300 + 300 + 200 + 100 +100=10005.
Таким образом, средневековые начальные арифметические операции (нумерация, удвоение, раздвоение), очевидно существовавшие в домонгольской Руси, сохранялись и впоследствии. Вероятно, не будет ошибкой считать, что их наличие в период татаро-монгольского ига было обусловлено достаточно развитой вычислительной культурой (с использованием абака), достигнутой Русью в предшествующий период.
Имеются косвенные данные о том, что в XII—XIV вв. счетное приспособление типа архаического абака на Руси употреблялось более широко, чем кажется на первый взгляд. Об этом говорит распространение знака для обозначения десятитысячного разряда. Так, этот символ — символ, представляющий собой букву «а» в кружке («тьма» = 10 тыс.), применялся в обычном тексте (нематематическом) как сокращенное обозначение слова «темнота». Чтобы такое обозначение употреблялось в церковной литературе, к которой обращались достаточно широкие круги грамотных людей, оно должно было быть обычным для древнерусского просвещенного человека.
В текстах - южнославянского происхождения, а также переводных греческих хронографических сочинениях, где встречались числа порядка десятков и сотен тысяч, применялась комбинированная форма записи — архаичная цифра в сопровождении слова «тьма». Особый энак десятитысячного разряда здесь не встречается (до XVI в.).
Факт «обычности» знака десятитысячного, разряда в письменной практике разъясняется на основе особенностей вычислительной «техники» с использованием восковых дощечек (цер), которые на Руси встречаются с конца XI в. Применяя особые обозначения для больших числовых разрядов, можно уместить на сравнительно небольшой восковой поверхности цер числа порядка сотен тысяч и десятков миллионов. Если вычисления производили на абаке, а промежуточные записи делали на вощечке, то с учетом небольших размеров последних и значительной величины чисел, которыми оперировали в Древней Руси уже на стадии обучения, символика десятитысячного разряда должна была иметь почти такую же известность, как 27 основных знаков нумерации.
В приведенной выше работе В. К. Кузаков справедливо отмечал, что привычная нам арифметическая система не зафиксирована ни в одном документе, в то же время источники («Учение» Кирика, «Русская Правда») свидетельствуют об умении выполнять арифметические действия с большими числами порядка сотен тысяч и десятков миллионов. Указанное парадоксальное положение полностью разъясняется, если исходить из представления о том, что в Древней Руси в качестве вычислительного средства использовался абак архаического типа с записью исходных и промежуточных данных на восковой дощечке. В таком случае никаких записей в привычной нам арифметической системе и не должно было быть, результаты вычислений «считывались» с абака (или церы) и записывались в виде окончательных итоговых чисел, независимо от их величины.
Можно представить в следующем виде древнерусского вычислителя за работой. Его «инструментами» были: маленький мешочек с вишневыми и сливовыми косточками, дощечка для писания по воску (цера) и «писало» — металлическая или костяная палочка, имевшая с одной стороны заострение, а с другой — лопаточку. Исходные числа, с которыми нужно было произвести вычисления, он заносил «писалом» на восковую поверхность церы. Отсутствие стола или скамейки его не смущало. В случае нужды древнерусский вычислитель выбирал ровный участок земли и проводил на нем «писалом» несколько вертикальных линий, разбивая счетное «поле» на колонки. В колонках он сперва раскладывал плодовые косточки в соответствии с числовой записью на цере, а затем по определенным правилам перемещал их. Получив искомый числовой результат, он переносил на церу полученное число. Так он поступал до тех пор, пока не исчерпывались исходные данные. Закончив вычисления, счетчик собирал косточки и складывал их в мешочек до следующего раза.
Арифметика Древней Руси сродни не современной арифметике начальной школы, а машинной математике. Если сейчас ее «лицо» определяют ЦЭВМ (цифровые электронные вычислительные машины), то арифметику Древней Руси можно отнести к категории ЦВМ (цифровых вычислительных машин) домеханического типа6.
В свете изложенного по-новому выступает роль арифметического знания в средневековой культуре домонгольской Руси в отношении ее «веса» в комплексе явлений, которые характеризуют особенность облика русского средневековья. Складывается впечатление, что «выход» вычислительной арифметики, в повседневную жизнь средневековой Руси был богаче, чем представлялось до сих пор.
В стране были вычислители, не только умевшие делать элементарные подсчеты, но и математики, хорошо владевшие этим вычислительным средством. В первом случае соответствующие знания (о записи чисел на абаке, о выполнении действий на нем и пр.) приобретались, по видимому, в рамках учебно-математического «фольклора»7. О том, каких успехов добивались на Руси в использовании абака, свидетельствует (сочинение Кирика, написанное 1136 г. Здесь ученый новгородец точно производит вычисления с гигантскими числами порядка десятков миллионов. Для подготовки математиков такого класса, как Кирик, нужны специальные учебные упражнения, содержащие большие числа. Они появились не позже XI—XII в., на что указывают упомянутые выше статьи-задачи, встречающиеся в отдельных списках «Русской Правды».
Таким образом, на Руси с XI—XII вв. вычислительная культура была достаточно высока. Древнерусский инструментальный счет впоследствии совершенствовался и модернизировался; его традиции сохраняются до настоящего времени в практике употребления русских (конторских) счетов.
1 Гнеденко В. В. Очерки по истории математики в России. М.—Л, Гостехтеориздат, 1946; Юшкевич А. П. История математики в России до 1917 г. М., «Наука», 1968.
2 Симонов Р. А. Математическая мысль Древней Руси. М., «Наука», 1977.
3 Кузаков В. К. Естественнонаучные представления на Руси (X— XV вв.). — «Вопросы истории», 1974, № 1, с. 127.
4 Голубева Л. А. Граффити и знаки пряслиц из Белоозера. — В кн.: Культура средневековой Руси. Л, «Наука», 1974, с. 19, рис. 2, пряслице 3.
5 См.: Симонов Р. А, Употребление «юса малого» в значении 1 тысячи в тайнописи XVII в. — «Зап. отд. рукописей Гос. б-ки СССР им. В. И. Ленина», 1974, вып, 35, с. 125.
6 Майстров Л. Е. Основные этапы развития вычислительных машин;—Труды XIII Международного конгресса по истории науки, секция V. М., «Наука», 1974, с. 100.
7 Симонов Р. А. Предыстория рукописной и печатной русской математической книги (древнерусский учебно-математический «фольклор» и «пособия» табличного тип). — Сб.: «Рукописная и печатная книга». М., «Наука», 1975, с. 205—212.
<< Назад Вперёд>>









